Understanding the Mole: Molecular Weights in Chemistry

In this article, we will discuss the significance of the mole in chemistry and how it is applied to chemical reactions and products.

Covered in this article:

• What is a mole in chemistry?
  • How moles are calculated
  • The relationship between Moles and molecular weights
• Using Moles to calculate chemical product percentages
• Conclusion

What is a Mole in chemistry?

The mole (or mol) is a quantity unit of measurement in chemistry that represents a very large, specific number of atoms, molecules, or ions.

The number of atoms/molecules in one mole is known as Avogadro's number, which is exactly 6.02214076 × 10²³. As arbitrary as this number seems, it is the number of atoms in exactly 12 grams of carbon.¹

The mole is important because it provides a bridge between atomic weight––which is too small to measure––and a weight we can physically measure. It converts theoretical mass into practical mass that can be used in a laboratory and beyond.

For instance, if we wanted to combine two Hydrogen atoms with one Oxygen to create water (H₂O), there is no spoon or set of tweezers small enough to do so. We need a LOT of atoms of each element. This is where the mole comes into play. If we know the exact number of grams per mole (g/mol), we can precisely measure the right ratio of atoms/molecules/ions to create a desired reaction.

Thankfully, molecular weights of almost every known substance have already been discovered and are public information.

How Moles are calculated

Moles = mass ÷ molecular weight

To determine the number of moles in a given sample, you divide the mass of the sample by the molecular weight of the substance. The molecular weight of every element is listed in the Periodic Table of Elements.

As you can see above, the molar weight of elemental chlorine is 35.45 g/mol. The Periodic table has every element's molar weight listed. This is helpful for elements, but most substances in our world are not simple elements––they are compounds of several elements.

Thanks to the mole, basic math can show us the molar weight of any compound.

The relationship between Moles and molecular weights

The molecular weight of a substance is the sum of the atomic weights of all the atoms in a molecule. It is expressed in atomic mass units (amu) or grams per mole (g/mol). By knowing the molecular weight of a substance, you can determine the number of moles present in a given mass and vice versa.

Let's demonstrate how to calculate the molecular weight of (H₂O). Here's the math:

[Hydrogen (1.0078 g/mol) x 2] + [Oxygen (15.999 g/mol)] = H₂O (? g/mol)
[2.0156 g/mol] + [15.999 g/mol] = H₂O (18.015 g/mol)

Taking this a step further, let's say we have 10 grams of water (H₂O), and we want to know how many moles of water that is.  We just divide the mass (10 g) by the molecular weight of water (18.015 g/mol). We find we have approximately 0.56 moles of water.²

Using Moles to calculate chemical product percentages

Moles are used to calculate chemical product percentages by comparing the number of moles of a specific component to the total number of moles in a mixture or reaction. This allows us to determine the percentage of ingredients in a given product.

Now let's apply moles and molar weights to swimming pool chemicals.

Many of the products we use in pools are fairly complex chemicals. The active ingredient may be one chemical compound, while there may be other additives in the product too. For instance, Trichlor (Trichloro-s-triazinetrione) products are usually labeled as 99%. But trichlor can also be sold in various other concentrations, like 53.5%. What do these numbers actually mean?

We will expand upon pool chemical product percentages in our next article, but for now, let's look at the molar weights of various compounds we use in swimming pools:

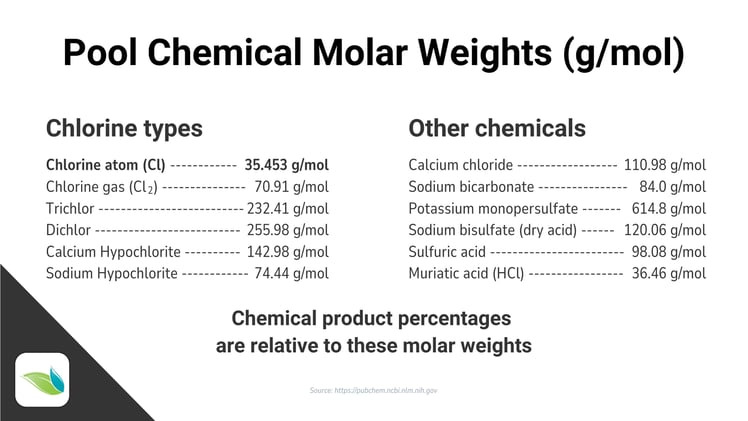
At the bottom of the graphic above, it says chemical product percentages are relative to these molar weights. This means the percentages listed on the label of pool chemical products we buy are based on the physical weight of the product itself relative to the molecular weight of the active compound.

For instance, pure chlorine is 35.454 g/mol, but different chlorine products show various concentrations of it. With math, we can discover the available chlorine percentage vs. the weight percentage of the product itself. Trichlor is an excellent example of this:

Pure trichlor has a molar weight of 232.41 g/mol. The product is usually labled "99% Trichloro-s-triazinetrione". Does that 99% mean it's 99% chlorine? No. It means the substance in the bucket is 99% trichlor.  To understand the percentage of available chlorine, we must compare the molar weight of chlorine to the molar weight of trichlor itself.

Chlorine (Cl) = 35.453 g/mol
Trichlor (C₃Cl₃N₃O₃) = 232.41 g/mol

There are three (3) chlorine atoms bound to CYA in trichlor, which means we multiply the weight of chlorine by 3:

3 x (35.453) = 106.359

Divide that by trichlor's molar weight to find the weight percentage of available chlorine in Trichlor:

106.359 ÷ (232.41) = 0.458 = 45.8% chlorine in trichlor (by weight) 

But since molecular chlorine (Cl₂) is what dissolves in water to create one active chlorine (Cl₂ + H₂O → HOCl + HCl), we need to multiply the 106.359 by 2, then divide that into the molar weight of trichlor to find the available chlorine percentage.

[2 x (106.359)] ÷ 232.41 = % available chlorine in trichlor
212.718 ÷ 232.41 = 0.915 = 91.5% available chlorine in pure trichlor

But remember, Trichlor is labled 99%, so we must multiply this available chlorine by 0.99, and we get 90.6% available chlorine in trichlor products.

Conclusion

The mole serves as a bridge between the theoretical and the practical. It allows us to compile enough matter to physically measure and handle. Thanks to chemists over the past few centuries, we know the molar weights of the entire periodic table of elements and most known compounds on earth.

Molar weights are expressed as grams-per-mole (g/mol). In other words, when we have one mole of a substance (6.02214076 x 10²³, or 602,214,076,000,000,000,000,000 atoms/ions/molecules), we can weigh it in grams. From there, it's just math to figure out product percentages, which we will explore in our next article.

¹  Agnew, H., Alivar-Agnew, M. 6.3 Counting Atoms by the Gram. Licensed by CK-12. 

²  National Center for Biotechnology Information (2023). PubChem Compound Summary for CID 962, Water.